Machine learning10 December, 2024

Linear Regression

Sơ lược về machine learning

Học máy (hay máy học) là 1 lĩnh vực thuộc trí tuệ nhân tạo, nghiên cứu và xây dựng các kỹ thuật để hệ thống học tự động từ dữ liệu nhằm giải quyết 1 vấn đề cụ thể nào đó.
Dựa vào tính chất của tập dữ liệu huấn luyện (training data) mà các nhà nghiên cứu thường phân các thuật toán của Machine learning ra làm 2 nhóm chính: học có giám sát (Supervised learning) và học không giám sát (Unsupervised learning).

Supervised learning: dữ liệu huấn luyện sẽ được quan sát và được gán nhãn (label) nhằm chỉ thị loại của dữ liệu. Ví dụ: bài toán phân loại trái cây chín/ sống, mỗi trái sẽ được gán cho 1 nhãn tương ứng. Sau khi huấn luyện hệ thống có thể dự đoán đầu vào $x$ (là 1 trái bất kỳ) cho ra đầu ra $y$ là chín hoặc sống.
Unsupervised learning: dữ liệu huấn luyện sẽ không được gán nhãn, thế nên không thể biết loại của từng điểm dữ liệu, bằng công cụ toán học, hệ thống sẽ trích xuất đặc trưng của dữ liệu đầu vào, tìm mối quan hệ giữa chúng, từ đó có thể gom chúng vào từng nhóm riêng biệt.

Supervised lại bao gồm 2 nhóm nhỏ là bài toán phân lớp (Classification) và bài toán dự đoán số (Numeric Prediction). Và supervised là nhóm phổ biến nhất trong các thuật toán machine learning.
Trong khi đó unsupervised bao gồm bài toán gom cụm (Clustering).

Linear regression

Linear regression (hồi quy tuyến tính) là mô hình thuật toán được xếp vào loại bài toán dự đoán số (Numeric Prediction). Và là một trong những thuật toán căn bản nhất, là tiền đề để chúng ta có thể đi tiếp được các thuật toán nâng cao hơn như mạng nơ-ron nhân tạo sau này (đây là quan điểm cá nhân của mình).

Đặt vấn đề và giới thiệu

Xuất phát từ thực tế ta có nhu cầu dự đoán giá nhà, giá chứng khoán hoặc dự báo thị trường lao động,... trong tương lai. Giả sử sau 1 năm ta thu thập được bộ dữ liệu về giá của 100 căn nhà bao gồm diện tích $x_1$ , vị trí $x_2$ ,... và giá $y$ . Câu hỏi đặt ra là liệu khi có người nhờ ta định giá 1 căn nhà mới với thông số $x_1$ , $x_2$ thì ta có thể dự đoán được giá $y$ của nó hay không? Bước đầu ta nhận định $y$ chính là hàm $f(x)$ (function) và cái mà chúng ta cần đi tìm chính là dạng của hàm này. Ở đây input của ta chính là [ $x_1$ , $x_2$ ] và output $y$ là 1 số liên tục (continuous value).
Hàm f sẽ có dạng như sau:

y = f(x) = w_1x_1 + w_2x_2 + w_0x_0 = \bold{x}^T\bold{w}

$\bold{w}$ = [ $w_1$ , $w_2$ , $w_0$ ] là vector hệ số (hay trọng số)
$\bold{x}$ = [ $x_1$ , $x_2$ , 1] là vector biến độc lập, ký hiệu T ở đây nghĩa là phép toán chuyển vị

Đến đây bạn đọc có lẽ sẽ thắc mắc tại sao lại có thêm $w_0$ và $x_0$ . Bạn đọc tiếp bên dưới mình sẽ giải thích thêm nhé.
Ta nhận thấy dạng của hàm này giống với đường thẳng $y = ax + b$ .

a: hệ số góc (coefficient) hay độ dốc (slope) của đường thẳng, giá trị này cũng chính là đạo hàm của hàm số
b: điểm tung độ (intercept) (là điểm mà đường thẳng cắt trục tung tại điểm này)

Bạn đọc có thể thấy rằng hệ số $w_0x_0$ bên trên chính là điểm tung độ b của đường thẳng. Nếu điểm này bằng 0 đường thẳng sẽ luôn đi qua gốc tọa độ $O(0,0)$ . Ta thêm $w_0$ nhằm tăng tính linh hoạt của mô hình và hệ số này còn được gọi là Bias.

$\rArr$ vector $\bold{w}$ chính là cái mà ta cần đi tìm, là tham số của mô hình. Thêm nữa dạng của hàm là đường thẳng thể hiện quan hệ tuyến tính và output là một mảng các số thực dương khác nhau. Nên tên gọi hồi quy tuyến tính xuất phát từ đây.

Sai số dự đoán

Ta gọi $\hat{y}$ (đọc là y hat) là giá trị ta đự đoán, trong khi đó $y$ là giá trị thực tế. Thế thì giữa 2 giá trị này tất có sai số. Ta gọi giá trị sai số là $e$ . Và áp dụng bình phương độ lỗi (squares of the error) như sau:

\begin{aligned} e &= (y - \hat{y})^2 = (y - \bold{x}^T\bold{w})^2 \\ \hArr e &= \dfrac{1}{2}(y - \bold{x}^T\bold{w})^2 \end{aligned}

Ta sử dụng bình phương nhằm tránh trường hợp độ lỗi là số âm.
Ta nhân thêm hệ số $\dfrac{1}{2}$ là nhằm triệt tiêu hệ số 2 sau khi lấy đạo hàm (ở bước kế tiếp bên dưới)

Hàm mất mát (loss function hay cost function)

Bởi vì ta có bộ dữ liệu gồm n điểm với từng cặp (input và output) nên phương trình trên sẽ trở thành:

\dfrac{1}{2n}\sum_{i = 1}^n(y_i - \bold{x}_i^T\bold{w})^2

Lý do phải chia n là vì ta tính tổng của n điểm, n quá lớn sẽ dẫn đến độ lỗi lớn và ta cần lấy trung bình cộng của chúng nhằm tránh điều này.

Và đây cũng chính là dạng của hàm mất mát của chúng ta:

L(\bold{w}) = \dfrac{1}{2n}\sum_{i = 1}^n(y_i - \bold{x}_i^T\bold{w})^2

Tối ưu hàm mất mát

Nhận thấy rằng dạng của hàm L liên quan đến chuẩn Euclidean $l_2$ (Euclidean $l_2$ - norm - chuẩn norm này nhằm đo khoảng cách giữa 2 vector/matrix) có dạng:

L(\bold{w}) = \| \bold{y} - X^T\bold{w} \|_2^2

Mình đã biến đổi [ $y_1$ , $y_2$ , ..., $y_n$ ] thành vector $\bold{y}$
và [ $\bold{x}_1$ , $\bold{x}_2$ , ..., $\bold{x}_n$ ] thành ma trận $X$
Mà $\|u\|_2^2 = u^Tu$

\begin{align} \rArr L(\bold{w}) = (\bold{y}-X^T\bold{w})^T(\bold{y}-X^T\bold{w}) \end{align}

Tiếp theo, do ta mong muốn trung bình sai số là nhỏ nhất => Cần tối thiểu hàm mất mát => Lúc này ta cần tính đạo hàm của hàm L theo w và giải phương trình đạo hàm bằng 0. Nghiệm tìm được chính là vector hệ số w cần tìm.
Lý do mà ta cần tính đạo hàm là vì ta cần khảo sát sự biến thiên của hàm số (giống như hồi còn làm toán phổ thông các bạn nhỉ ^^) và cần tìm ra điểm $w$ là cực tiểu (còn gọi là điểm cực trị), điểm mà tại đó giá trị đạo hàm của nó bằng 0 và giá trị của hàm số đạt cực tiểu.
Ta lại có: $\Delta_x(Ax - b)^T(Ax - b) = 2A^T(Ax - b)$ (theo bảng công thức đạo hàm vector - matrix) (2)
Từ (1) và (2) suy ra:

\begin{aligned} \dfrac{\Delta L(\bold{w})}{\Delta \bold{w}} &= \dfrac{1}{2n}2X(X^T\bold{w} - \bold{y}) \\ &=\dfrac{1}{n}X(X^T\bold{w} - \bold{y}) \\ &\hArr \dfrac{1}{n}X(X^T\bold{w} - \bold{y}) = 0 \\ &\hArr \bold{w} = \dfrac{X\bold{y}}{XX^T} \\ &\hArr \bold{w} = (XX^T)^{-1}X\bold{y} \end{aligned}

Ta đặt $A = (XX^T) \rArr A^{-1}$ là phép tính nghịch đảo ma trận. Để tính phép tính này ta dùng hàm linalg.pinv() có sẵn trong thư viện numpy (ngôn ngữ python).

Ví dụ với ngôn ngữ python

Ví dụ mình cần xây dựng 1 mô hình đơn giản có thể dự đoán tiền lương dựa trên đầu vào là số năm kinh nghiệm của 1 người (ngoài thực tế cần nhiều yếu tố khác nữa chứ không chỉ dựa vào số năm kinh nghiệm). Giả sử mình đã thu thập được 15 mẫu dữ liệu (dataset) như bảng bên dưới, các bạn có thể download full data tại kaggle:
Data table

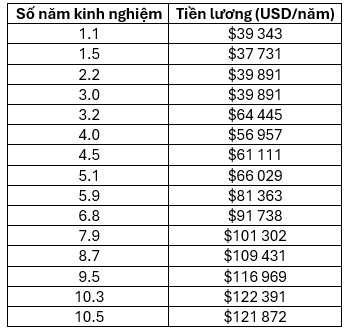
Mình sẽ chỉ lấy 13 mẫu dữ liệu làm tập dữ liệu huấn luyện, 2 mẫu còn lại bao gồm (9.5 và 10.3) sẽ được dùng để kiểm thử (test) mô hình của ta.
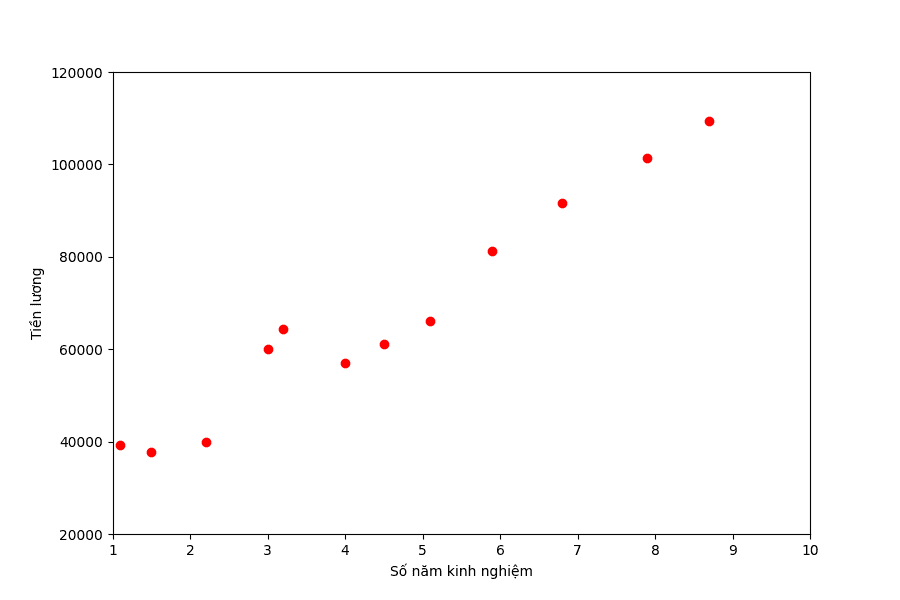
Đầu tiên ta sẽ biểu diễn bộ dữ liệu này (13 mẫu) trên hệ trục tọa độ trước nhé:

from __future__ import print_function
import numpy as np
import matplotlib.pyplot as plt
# years experience 
rawX = np.array([[1.1, 1.5, 2.2, 3.0, 3.2, 4.0, 4.5, 5.1, 5.9, 6.8, 7.9, 8.7, 10.5]])
X = rawX.T
# Salary
y = np.array([ 39343, 37731, 39891, 60150, 64445, 56957, 61111, 66029, 81363, 91738, 101302, 109431, 121872])
# Visualize training data 
plt.figure(figsize=(9,6))
plt.plot(X, y, 'o')
plt.axis([1.0, 10, 20000, 120000])
plt.xlabel('Số năm kinh nghiệm')
plt.ylabel('Tiền lương')
plt.show()

Nhận thấy rằng các điểm dữ liệu của ta có xu hướng phân bố hội tụ về 1 đường thẳng nên có thể áp dụng được thuật toán hồi quy tuyến tính. Tiếp theo ta sẽ thiết lập mô hình:

# Building Xbar 
one = np.ones((X.shape[0], 1))
Xbar = np.concatenate((one, X), axis = 1) # each point is one row 
# Calculating weights of the fitting line 
A = np.dot(Xbar.T, Xbar)
b = np.dot(Xbar.T, y)
w = np.dot(np.linalg.pinv(A), b)
# weights
w_0 = w[0]
print(w_0)
w_1 = w[1]
print(w_1)

Kết quả ta thu được $w_1$ và $w_0$ lần lượt là [25359.715259859884, 9342.96120530778] (mình gọi là bộ trọng số).
Tiếp theo ta sẽ test thử với bộ dữ liệu (9.5 và 10.3)

y1 = w_1*9.5 + w_0
print(y1)
y2 = w_1*10.3 + w_0
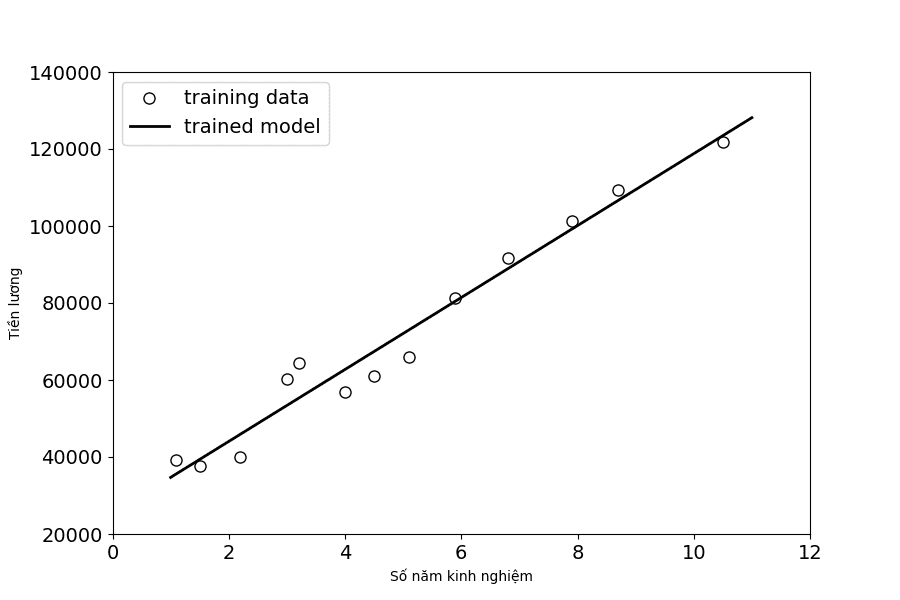
print(y2)

Kết quả $y_1$ $\approx$ 114 118 và $y_2$ $\approx$ 121 592. Kết quả cũng tương đối gần với đáp án của ta [116 969, 122 391]. Đoạn code sau đây sẽ biểu diễn đường thẳng của mô hình chúng ta vừa huấn luyện (fitting line):

# Visualize all data 
x0 = np.linspace(1., 11, 2, endpoint=True)
y0 = w_0 + w_1*x0
plt.figure(figsize=(9,6))
plt.plot(X, y, 'o', color = 'white', mec = 'k', markersize = 8, label = "training data")      
plt.plot(x0, y0, color = 'k', linewidth = 2, label = "trained model")           
plt.axis([0, 12, 20000, 140000])
plt.xlabel('Số năm kinh nghiệm')
plt.ylabel('Tiền lương')
plt.tick_params(axis='both', which='major', labelsize=14)
plt.legend(loc = "best", fontsize = 14) 
plt.show()

Đôi khi với ma trận dữ liệu có kích thước lớn, việc tính ma trận nghịch đảo như trên sẽ gặp bất lợi thế nên ta còn có 1 cách khác để tìm $\bold{w}$ mà không phải tính ma trận nghịch đảo, đó chính là thuật toán có tên gradient descent.

Các dạng khác của regression

Polynominal regression (hồi quy đa thức)
Generalized linear model: Logistic regression, Poisson regression
Log-linear models
Regression trees and model trees

Phân biệt giữa Classification và Numeric Prediction

Classification: là bài toán chúng ta cần xác định nhãn cho các điểm dữ liệu và đầu ra là các giá trị rời rạc (discrete) như các nhãn dùng để phân loại (categorical class label). Ví dụ: nhãn A/B/C hoặc nhãn là true/false trong phân lớp nhị phân,...
Numeric Prediction: dùng model để dự đoán các giá trị liên tục (continuous value) và không giới hạn. Ví dụ chiều cao, cân nặng, giá cả,... Và các vấn đề liên quan đến các giá trị liên tục này được xếp vào loại regression problem.

Tài liệu tham khảo

Vector and matrix norms
Matrix calculus
Sách Machine Learning cơ bản - Vũ Hữu Tiệp
Machine Learning Specialization - Andrew Ng
Data Mining - Concepts and Techniques - Jiawei Han, Micheline Kamber, and Jian Pei